BBFT: иерархический византийский отказоустойчивый консенсусный алгоритм

BBFT: иерархический византийский отказоустойчивый консенсусный алгоритм

ByStack Team

v1.0

1. Введение

Консенсус — это процесс, применяемый узлами для достижения окончательного соглашения о состоянии сети. Византийские отказоустойчивые (BFT) консенсусы считаются хорошо подходящими для блокчейнов с разрешенными правами, где между узлами существует полувысок. Консенсус BFT может обеспечить высокую TPS (транзакций в секунду), в то же время гарантируя безопасность при максимальномп-1/3) из общего N узлы одновременно неисправны.

PBFT (практическая византийская отказоустойчивость) является одним из широко распространенных принципов BFT (6). Тем не менее, это не хорошо масштабируется из-за О(N²) сложность общения. В этом отчете мы представляем иерархический алгоритм консенсуса BFT — BBFT. Он использует топологию сети для эффективного распределения и агрегирования сообщений между узлами и обеспечивает О(N) сложность общения.

2 Модель системы

Мы определяем систему как асинхронную распределенную среду, в которой отдельные узлы взаимодействуют через сеть точка-точка. Сеть может не доставлять сообщения, задерживать их (не на неопределенный срок) или доставлять их не по порядку. Сеть сама по себе неоднородна, что означает, что качество связи между узлами не одинаково и не остается постоянным между одним и тем же набором узлов.

Аутентификация сообщений гарантируется асимптотической безопасностью посредством криптографических подписей и хэш-функций (15, 17, 12).

Мы называем узел узел согласия если он участвует в процессе консенсуса. Узел консенсуса копирует текущее состояние системы. Узел шлюза является консенсусным узлом, который выполняет дополнительное агрегирование подписи. Лидер узел является консенсусным узлом, который предлагает блок для проверки в начале раунда консенсуса. Каждый узел обладает уникальным идентификатором и известен другим узлам.

Мы называем узел византийский узел если он ведет себя произвольно. Это может задерживать связь, изменять сообщения, воспроизводить сообщения и подделывать подписи. Византийские узлы могут даже вступать в сговор. Мы предполагаем, что неисправные узлы связаны в вычислительном отношении, так что невозможно подорвать криптографические методы, используемые для защиты сообщений.

Узлы организованы в виде вершин дерева, причем ребра являются путями связи, как показано на рисунке 1. Неконечные узлы являются узлами шлюза, а конечные узлы являются узлами консенсуса. Узлы шлюза верхнего уровня связаны друг с другом. Лидерный узел всегда является одним из узлов шлюза верхнего уровня.

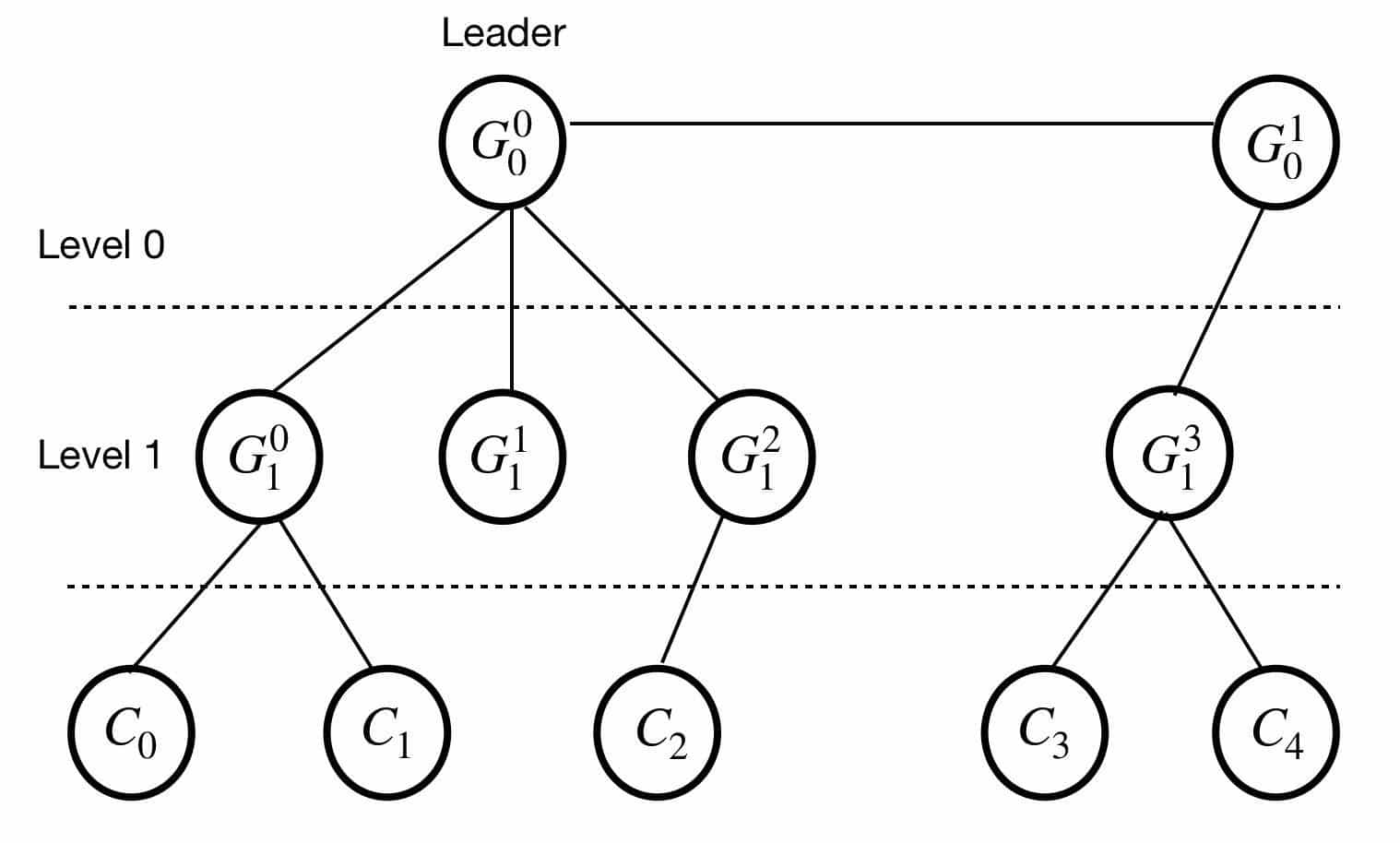
Рисунок 1: Пример Узлы Топология соединения

Система Византийская ошибка терпимая с минимальным количеством узлов N = 3е +1 до е узлы неисправны. Это число обеспечивает более низкий порог, потому что в худшем случае е неисправные узлы, узел должен быть в состоянии продолжить N — е ответы, несмотря на то, что е неотвечающие узлы на самом деле не неисправны. Это требует N — 2f> f, Следовательно n> 3е,

В следующих разделах мы опишем процесс достижения узлами консенсуса. Затем мы обсудим два важных компонента алгоритма: как сеть разделена и как эффективно собирать подписи.

3 Процесс консенсуса

Процесс согласования напоминает типичный PBFT (6) с дополнительной обработкой агрегации сигнатур на узлах шлюза. В обычном случае алгоритм состоит из трех этапов: распространять, совокупный, а также завершать как показано на рисунке 2.

Рисунок 2: Пример согласованного процесса единой сети с пятью узлами

В начале раунда консенсуса узлы имеют одинаковый номер представления v = 0, а высота блока час, Каждый узел имеет свой уникальный идентификатор я, который известен другим узлам. Растровое изображение м используется во время передачи сообщений, чтобы указать, какие подписи узлов включены в агрегированную подпись.

1. Лидерный узел п выбирает транзакции из своего пула транзакций и упаковывает их в следующий предложенный блок б, Предложение транслируется его равноправным узлам шлюза на том же уровне, что и <DISTRIBUTE, H, V, т, Ь, Ь_σ>.
2. Его равноправные узлы шлюза получают предложение и начинают передавать его по краям дерева топологии. Это завершает распространять этап.
3. На уровне листа, после получения предложения, узел консенсуса я проверяет блок и подпись, подписывает блок и отправляет результат на узел родительского шлюза как <AGGREGATE, H, V, м, б_σ>
4. На каждом неконечном уровне узлы шлюза проверяют полученные подписи от своих дочерних элементов, постепенно объединяют их со своими собственными и передают по краям дерева топологии.
5. Когда узлы верхнего уровня получают агрегированные подписи, они выполняют полный обмен сообщениями. Это завершает совокупный этап,
6. Полностью агрегированная подпись затем передается по краям топологического дерева, чтобы достичь конечных узлов как <FINALIZE, H, V, м, б_σ>.
7. Любой консенсусный узел при получении как минимум N — е подписи, достигает консенсуса и записывает блок в свой регистр. Это завершает завершать этап.

Консенсусный узел может инициировать VIEW-CHANGE предложение, когда оно не может достичь консенсуса в рамках T интервал времени, был предложен недопустимый блок или получена недопустимая агрегированная подпись. Вот T выбирается как максимальное согласованное время процесса и зависит от количества узлов и характеристик сети. Когда какой-либо узел получил хотя бы N — f ОБЗОР сообщения с тем же номером представления от других узлов, текущий номер представления обновляется и начинается новый раунд согласования.

Позволять N быть числом узлов консенсуса, и м число узлов шлюза верхнего уровня, общее количество сообщений, переданных в процессе согласования, составляет λ = m² — 2м + 3N — 2. Когда 1 ≤ м ≤ √N ⇒ λ ≤ 4N — 2√N — 2, процесс λ знак равно м сложность связи О(N). Многоуровневые шлюзовые узлы не влияют на общую сложность, потому что только узлы шлюза верхнего уровня выполняют полный обмен сообщениями. BBFT проявляет свою гибкость, когда м изменения. Как два особых случая BBFT, когда м = 1, BBFT становится FBFT (16), и когда м знак равно NBBFT становится PBFT.

4 Сетевое зонирование

Мы определяем граф топологии в качестве логического представления взаимосвязи между узлами. Узлы — это вершины графа, а ненаправленные ребра — это пути связи между узлами, а его вес — это задержка связи. Мы определяем дерево топологии как минимальное связующее дерево (MST), которое соединяет все узлы вместе, без каких-либо циклов и с минимально возможной общей задержкой. Мы считаем топологическое дерево уникальным, учитывая тот факт, что в реальных случаях использования задержка не может быть одинаковой между любыми двумя парами соединенных узлов.

Нахождение MST неориентированного графа является хорошо изученной областью (14, 7, 10). Существуют высокооптимальные алгоритмы линейной сложности (8, 13). Существуют также распределенные решения с линейной сложностью, где узлы полностью отключены и обмениваются данными только посредством передачи сообщений (9, 1). Чтобы построить MST в BBFT, мы можем либо развернуть выделенную службу, которая запрашивает номера задержки у узлов и возвращает MST обратно узлам, либо можно применить распределенный алгоритм. Обратите внимание, что даже при централизованном подходе внутренняя реализация сервиса может быть прозрачной для узлов. Детализация алгоритма выходит за рамки этого отчета.

После построения MST дерево поворачивается так, что выбранный узел-лидер находится на верхнем уровне, а количество узлов шлюза верхнего уровня не превышает √N, Учитывая динамику состояния межсетевого взаимодействия, дерево топологии периодически перегенерируется. Частота повторной генерации зависит от варианта использования и согласовывается с выбором лидера.

5 Подпись Агрегация

Когда узел шлюза получает ответы от своих дочерних согласованных узлов, он выполняет агрегацию сигнатур перед маршрутизацией сообщения. Наивная агрегация просто объединит все подписи вместе, что может привести к большому размеру сообщения и потребует, чтобы получатель проверил все подписи. Мы называем ключевую агрегацию эффективный если

1. Совокупный размер ключа должен оставаться относительно постоянным независимо от количества участников.
2. Время проверки ключа должно оставаться относительно постоянным независимо от количества участников.

Здесь термин «ключ» может относиться к любым типам примитивов, таким как секретные ключи, открытые ключи, подписи и т. Д

В BBFT мы используем мультисигнатурную схему BLS (Boneh-Lynn-Shacham) (4, 5, 3) для эффективного агрегирования подписей. С BLS можно объединять все типы примитивов, и результатом всегда является другой допустимый примитив. Примитивы, которые уже были агрегированы, также могут дополнительно агрегироваться постепенно, независимо от порядка, в котором это происходит. С этим свойством агрегированный размер подписи остается постоянным независимо от количества участвующих подписей. Еще одно уникальное свойство BLS заключается в том, что это можно сделать за один раунд, в отличие от схемы подписи Шнорра (11), где требуется настройка предварительной фиксации, которая приводит к нескольким раундам связи. Эта функция делает его идеальным для распределенной среды, не требующей доверия.

Позволять N быть количество участников, м быть сообщением, передаваемым между ними. Схема агрегации сигнатур BLS в BBFT работает следующим образом:

Операция сопряжения, как известно, является дорогой, она на порядок медленнее, чем типичная ECDSA, такая как сигнатура Шнорра (2, 11). Однако в случае одного и того же сообщения количество сопряжений ограничено 2 для каждой проверенной агрегированной подписи независимо от количества входных подписей.

6. Заключение

Мы представляем BBFT, эффективный византийский отказоустойчивый консенсусный алгоритм. Модель достигает О(N) сложность связи с определенным ограничением количества узлов шлюза. Стоит отметить, что предлагаемые здесь методы зонирования и агрегирования в качестве очень гибкой и реконфигурируемой модели не обязательно являются единственными вариантами выбора. В зависимости от реального варианта использования другие методы могут быть легко интегрированы в модель консенсуса.

Рекомендации

(1) Б. Авербух. «Оптимальные распределенные алгоритмы для связующего дерева с минимальным весом, подсчета, выбора лидера и связанных с этим проблем». В: Материалы девятнадцатого ежегодного симпозиума ACM по теории вычислений, STOC ’87. Нью-Йорк, Нью-Йорк, США: ACM, 1987, с. 230–240. ISBN: 0-89791-221-7. DOI: 10.1145 / 28395.28421. URL: http://doi.acm.org/10.1145/28395.28421.

(2) Александр Блок. BLS: это действительно так медленно? URL: https: // блог. dash.org/bls-is-it-really-that-slow-4ca8c1fcd38e. (Доступ: 05.21.2019).

(3) Дэн Бонех, Ману Драйджверс и Грегори Невен. «Компактные мультисигнатуры для меньших блокчейнов». В: Достижения в криптологии — ASIACRYPT 2018, Издание Томас Пейрин и Стивен Гэлбрейт. Cham: Springer International Publishing, 2018, с. 435–464. ISBN: 978-3-03003329-3.

(4) Дэн Бонех, Бен Линн и Ховав Шахам. «Короткие подписи от Weil Pairing». В: Материалы 7-й Международной конференции по теории и применению криптологии и информационной безопасности: достижения в криптологии, ASIACRYPT ’01. Берлин, Гейдельберг: Springer-Verlag, 2001, с. 514–532. ISBN: 3-540-42987-5. URL: http: //dl.acm.org/citation.cfm?id=647097.717005.

(5) Dan Boneh et al. «Совокупные и достоверно зашифрованные подписи на билинейных картах». В: Материалы 22-й Международной конференции по теории и применению криптографических методов, EUROCRYPT’03. Варшава, Польша: Springer-Verlag, 2003, с. 416–432. ISBN: 3-540-14039-5. URL: http://dl.acm.org/citation.cfm?id= 1766171.1766207.

(6) Мигель Кастро и Барбара Лисков. «Практическая Византийская Терпимость». В: Материалы третьего симпозиума по разработке и внедрению операционных систем, OSDI ’99. Новый Орлеан, Луизиана, США: Ассоциация USENIX, 1999, стр. 173–186. ISBN: 1-880446-39-1. URL: http://dl.acm.org/citation.cfm?id=296806.296824.

(7) В. Дейкстра. «Заметка о двух проблемах в связи с графиками». В: Нумерище Математик 1.1 (декабрь 1959 г.), с. 269–271. ISSN: 09453245. DOI: 10.1007 / BF01386390. URL: https://doi.org/10.1007/ BF01386390.

(8) Майкл Л. Фредман и Роберт Эндре Тарьян. «Кучи Фибоначчи и их использование в улучшенных алгоритмах оптимизации сети». В: ACM 34.3 (июль 1987 г.), с. 596–615. ISSN: 0004-5411. DOI: 10.1145 / 28869.28874. URL: http://doi.acm.org/10.1145/28869.28874.

(9) Г. Галлагер, П. А. Хамблт и П. М. Спира. «Распределенный алгоритм для остовных деревьев минимального веса». В: ACM Trans. Программа. Lang. Сист. 5.1 (январь 1983 г.), с. 66–77. ISSN: 0164-0925. DOI: 10.1145 / 357195.357200. URL: http://doi.acm.org/10.1145/ 357195.357200.

(10) Джозеф Б. Крускал. «О кратчайшем связующем поддереве графа и проблеме коммивояжера». В: Труды Американского математического общества 1 (1956), с. 48–50. ISSN: 00029939, 10886826. URL: http://www.jstor.org/stable/2033241.

(11) Грегори Максвелл и соавт. «Простые мульти-подписи Schnorr с приложениями для Биткойн». В: Дизайн, коды и криптография (Февраль 2019 г.) DOI: 1007 / s10623-019-00608-х.

(12) Альфред Дж. Менезес. Криптосистемы с открытым ключом эллиптической кривой, Норвелл, Массачусетс, США: Kluwer Academic Publishers, 1994. ISBN: 0792393686.

(13) Сет Петти и Виджая Рамачандран. «Оптимальный алгоритм минимального остовного дерева». В: ACM 49,1 (январь 2002 г.), с. 16–34. ISSN: 0004-5411. DOI: 10.1145 / 505241.505243. URL: http://doi.acm.org/10.1145/505241.505243.

(14) C. Прим. «Кратчайшие сети связи и некоторые обобщения». В: Технический журнал Bell System 36,6 (ноябрь 1957 г.), с. 1389–1401. ISSN: 0005-8580. DOI: 10.1002 / j.1538-7305.1957.tb01515.x.

(15) Л. Ривест, А. Шамир и Л. Адлеман. «Способ получения цифровых подписей и криптосистемы с открытым ключом». В: Commun. ACM 21.2 (февраль 1978 г.), с. 120–126. ISSN: 0001-0782. DOI: 10.1145 / 359340. 359342. URL: http://doi.acm.org/10.1145/359340.359342.

(16) Команда Гармонии. Техническая документация Harmony, URL: https: // гармония. один / whitepaper.pdf. (Доступ: 05.21.2019).

(17) Джин Цудик. «Аутентификация сообщений с односторонними хэш-функциями». В: SIGCOMM Comput. Commun. Rev. 5 (октябрь 1992 г.), с. 29–38. ISSN: 0146-4833. DOI: 10.1145 / 141809.141812. URL: http: // doi. acm.org/10.1145/141809.141812.

 

BBTF — это консенсусный алгоритм, принятый Bystack, платформой BaaS (Blockchain как услуга), разработанной Bytom. Алгоритм открыт для обсуждения для лучшего развития Bytom.